The Nephite system of currency was a binary system. This is manifested by how the values of each coin or measurement were twice the value of a lower denomination or half the value of the upper denomination. The advantage of a binary system is that it becomes easy to do mathematical functions on the numbers. Adding in particular becomes easy.

One odd part of the currency system is the gold limnah and the silver onti, whose value is reckoned as the value of “them all.”
Limnah = senine + seon + shum
Onti = senum + amnor + ezrom

In an intangible binary system, there is no need for a denomination that specifically represents a cumulative value of all the lesser ones. However, when the denominations stand for something heavy and tangible like silver or gold, there is an advantage of convenience in being able to exchange a large amount of metal for a small amount of metal. This makes it easier to carry large sums.

But this is not the whole reason for the gold limnah and the silver onti. The main reason lies in accounting and carrying numbers. Again, adding two binary numbers is pretty easy. (Below, I have used the silver denominations in my examples.)



What if you have to add lots of binary numbers? (People who collected taxes or fees or tribute would have to do this.) The larger the sums, the more likely you will have carry bits that slosh outside the range of your reckoning.







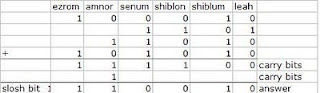
The function of the silver onti (and the gold limnah) were to flush the higher reckoning columns of digits so that no sneaky carry bit would escape their system. First they would bleed the higher denomination columns of bits (represented by the blue numbers). When they could no longer make ontis, they knew they could start adding.











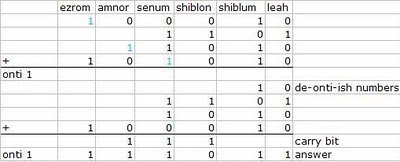
In summary, the denomination of the gold limnah and silver onti were designed to cope with the inevitable carry bits that would result from adding together large sums.
Continue reading at the original source →